2021-Survey-A Comprehensive Survey on Transfer Learning (Part3) Feature Transformation Strategy

https://ieeexplore.ieee.org/document/9134370

長いので分割することに。

全編の目次はこちら。

この記事はIntroduction, Related Work, Overview, Data Based ApproachのInstance Weighting Strategy。

Data Based Interpretation

Feature Based

Feature Basedについての手法紹介。

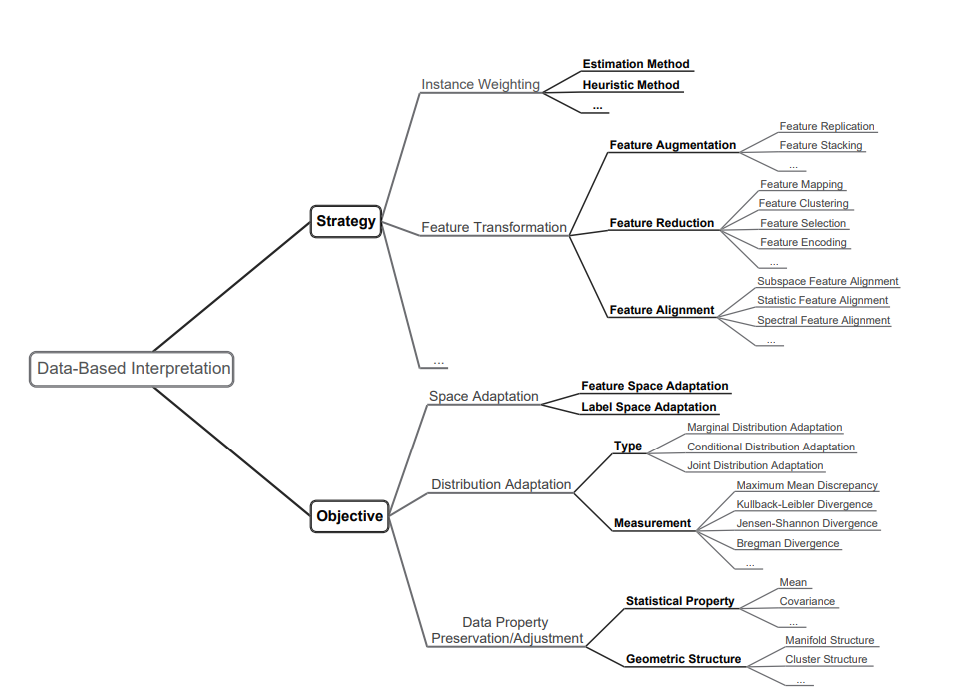
特徴量をうまく変換することで知識のTransferを実現する。具体的にはFeature Augmentation, Feature Reduction, Feature Alignmentの3つがある。上図のようにその上にもいろいろある。

Distribution Difference Metric

2つの分布が特徴空間に写像したときの距離を測りたい。それができれば、どれだけ動かせば重ねられるかがわかる。

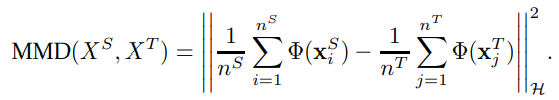
ここでは同じ変換関数(一般的にはカーネル関数でヒルベルト空間上に)に写像し、そのうえでの分布の重心の距離を測るというもの。

実際の推定はこれをそのまま展開して求めるというもの。

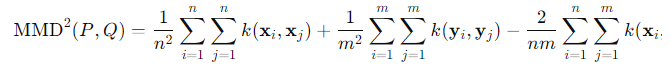
具体的には、以下のような指標がある。

KLダイバージェンス
ワッサースタイン距離
JSダイバージェンス
Bregmanダイバージェンス
ヒルベルト・シュミット独立基準
Maximum Mean Discrepancy

Feature Augmentation

元の特徴量を新しい特徴量に変換し、ソースドメインとターゲットドメイン両方の情報を統合する。

一番簡単な一例としては、単純に $[\mathbf{x}_i^S, \mathbf{x}_i^T]$ を結合させるとか。

Feature Augmentation Method(FAM)

論文: https://arxiv.org/abs/0907.1815

解説: http://bin.t.u-tokyo.ac.jp/rzemi19/file/13_iizuka.pdf

まさにそのまま結合というのをやっている。一般的な特徴、ソースドメイン特有の特徴、ターゲットドメイン特有の特徴の3つからなると考える。

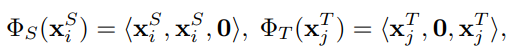
それぞれの特性をそれぞれの次元で保持しつつも、全く同じ次元に2つのドメインの特徴量をマッピングしているので、理論上はこれで十分な学習能力があればDomain Adaptationできる。

しかし、あきらかに冗長であり、もっと次元を落としての学習ができるというのは正直なところである。

ただし、上の変換で見るとわかるように、これはソースとターゲットが同じ特徴空間の上にあるとき=Homogeneous限定であり、たとえ0とかで埋めて次元をそろえても、このままだとHeterogeneousでは訓練が難しいという現実がある。

Heterogeneous Feature Augmentation

論文: https://arxiv.org/abs/1206.4660

上の問題を解消するための手法。次元をそろえるために、それぞれ $W^S, W^T$ という行列を乗じさせる。これで行列を学習できれば、実質1つの特徴空間へマッピングしていることになるが、そんなうまくいくことは難しいよね。

もちろんこれを深層学習の学習器で代替してもいい。

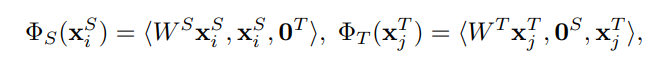
Feature Mapping

いわゆる、正真正銘同じ特徴空間に写像する。先ほどのHFAの行列を用意するのも実質的にFeature Mappingである。

マッピングの目標は、低次元の写像関数 $\Phi$ を定義して以下のものを最小化することである。DISTは2つの分布の距離、VARは $\Phi$ によってマッピングされた二つの分布から得たデータの分散。

つまり、距離は小さければ小さいほどうれしいし、分散は大きければ大きいほど明確に分かれているのでうれしい。

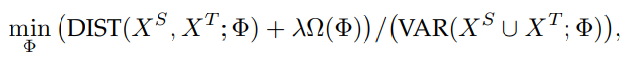
これの最大化をやるにあたって、まずは分子の最小化をしてから、分母の最大化を行う。これはPCAなどを使えばいい。

次に、どのように $\Phi$ を見つけるのかを考える。主に3つの考えがある。

Mapping Learning + Feature Extraction

高次元空間を最初に定義し、カーネル法でそこに写像する。そのために写像する変換をまず、カーネル法の $\sigma$ などを適切な値にするべく学習する。つまりハイパーパラメタの学習で、ガウシアンカーネルなら決まった $\sigma$ で変換して得た特徴量で一連の学習を行い、それが一番良い結果をもたらした $\sigma$ を使うということ。

カーネル行列を求めたら、PCAなどで影響の少ない次元を削り落とす。これはカーネルPCAという。固有ベクトルのうち固有値が大きいものから順に、 $U$ に並べる(必要な次元のぶんだけ)

Z = U^T K

この $Z$ がマッピングした特徴量であり、これを使い学習を行う。

Mapping Construction + Mapping Learning

同様にカーネル行列を構築する。先ほどはPCAで次元を落としていたが、ここでは別の高次元から低次元へ変換する変換行列 $W$ などを学習し、予測するべきラベルとの差を最小化する。

\min_W ||KW - Y||

これが学習できたならば、 $KW$ でラベルを得ることができる。

Direct Low-dimensional Mapping Learning

低次元マッピングが線形であると仮定して、カーネル行列に変換せずに直接ラベルに変換する。

\min_W \sum_{i=1}^n || W \mathbf{x}_i - \mathbf{y}_i ||^2

つまり今までのカーネル法云々の議論は不要で、実は低次元でそのままできてしまうというならそれに越したことはない。

データの構造を保持したまま学習するには

以上のものは線形写像などで計算しているが、データの構造に関して保持をしないという問題がある。これについて、以下のような式で定式化をできる。

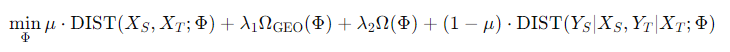
第一項はソースとターゲット間のサンプルを、 $\Phi$ でできるだけ近くに写像するというもの。これは周辺分布
第二項は $\Phi$ について、構造を保持するために追加した幾何的な正則化項。
第三項は一般的な写像関数の複雑度を制御する $\Phi$ である。
第四項は第一項と重み的には合成してしており、ソースとターゲット間の $Y|X$ の条件付き分布が一致することを目指している。

この手法では、制約条件として以下のものである。この制約では、 $\Phi(X)$ が新しい特徴表現であり、 $H$ は対角線だけ $(n-1)/n$ でそれ以外は $-1/n$ でありこれが中心化行列。

中心化行列を乗じると、データを原点中心に中心化して平均0にできる。

なので、制約の2つ目の式は中心化された散布行列である。これをつけると幾何的な特性を保持しやすくなる。

H = I - \frac{1}{n} \mathbf{1} \mathbb{R}^{n \times n} \\ \Phi(X) ^ T H \Phi(X) = I

これを用いることで、

各特徴軸に対する分散が均等になる。
各軸に沿ったデータの分散が最大化される。
クラス間の距離が最も遠くなるようにできる。

なお、Target Domainではラベルがないことが常なので、その場合はCo-training、Tri-trainingなどで自己教師あり学習を行い、Pseudo Labelを付与する。

なお、以下の式の特別な $\mu, \lambda_1$ などについては以下のようなものがある。

$\mu = 1, \lambda_1 \neq 0$

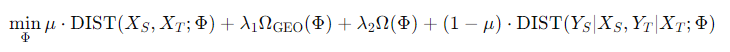
論文: https://repository.hkust.edu.hk/ir/Record/1783.1-20102

この時、以下のような目的関数になる。

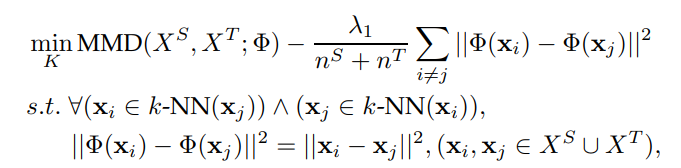
MMDを距離として扱う。 $\mu$ では分布間の距離のみを考慮し、条件付分布 $p(y|\mathbf{x})$ の距離は考えない。そして、ここでの幾何学的な特性による制約は、

もともとの特徴空間での距離を、新しい特徴空間上での保存させる。
$\mathbf{x}_i, \mathbf{x}_j$ は同じDomainから選ばれている。TargetはTarget、SourceはSourceと比べている。
- 統合されたデータセットで考えることもできる(特にSource DomainとTarget Domainは同じ特徴空間上にあるならば)

分散行列による制約に変わりにこれを導入した。

$\mu= 1 , \lambda_1=0$

Transfer Component Analysis

論文: https://ieeexplore.ieee.org/document/5640675

この時、以下のような目的関数になる。

\min _K MMD(X^S, X^T; \Phi)

単純に $p(\mathbf{x})$ の分布を合わせるだけである。

カーネル行列を学習したあとにPCAをするMMDEとは異なり、Transfer Component Analysis(TCA)はMapping Construction Mapping Learningにあるようにやっているだけ。

$\mu=0.5, \lambda_1=0$

Joint Distribution Adaptation

論文: https://ieeexplore.ieee.org/document/6751384

幾何的な特性を考慮せずに、 $p(\mathbf{x}), p(y|\mathbf{x})$ の分布が同じウェイトでのマッピングを計算しようとしている。

\min _K MMD(X^S, X^T; \Phi) + MMD(Y^S|X^S, Y^S|X^T; \Phi)

これを実現するためには、Target Domainにもラベルがないといけない。ただないのが普通なので、Source Domainで学習して特徴空間を調整し、 $p(\mathbf{x})$ の分布を密度比で推定させたものを使って、まずはPseudo LabelをTarget Domainのものに付与する。

次に、Pseudo Labelを使って条件付ラベル分布を比較しておき、特徴空間をさらに調整する。

これ動きを1セットとして何回も繰り返す感じ。

ようわからん……..

📄2013-IEEE-Transfer Feature Learning with Joint Distribution Adaptation

$\mu \in (0, 1), \lambda_1 = 0$

Balanced Distribution Adaptation

論文: https://arxiv.org/abs/1807.00516

上記のJDAの拡張である。JDAと違い、周辺分布と条件付ラベル分布の距離は1:1の重みではなく自由に動かせる。また、Weighted MMDというのを提案している。これはMMDを計算するときクラスの不均衡を考えて、各サンプルに重み $w_i^T, w_i^S$ を与えたもの。